Eco-evolutionary modeling with GEMs (Gillespie eco-evolutionary models)
This site is your home for information, code, and examples of Gillespie eco-evolutionary modeling. Please contact me (jpdelong ‘at’ unl ‘dot’ edu) for clarification of any text, code, or figures. The site is new in 2018, and I will update it regularly until it is sufficient to get a new user up and running GEMs. All of the code used here is for Matlab. There are efforts underway to develop GEM code for R and this code will be posted when ready.
What are GEMs?
GEMs are a computational analogue to natural selection. Key features of GEMs are: 1) fitness-influencing traits of individuals guide population dynamics (but GEMs are not individual-based models), 2) fitness landscapes inherent to a particular model determine which traits will be favored in the population, 3) demographic (including individual) stochasticity influences outcomes, and 4) trait distributions and variance are continually updated.
How do GEMs work?
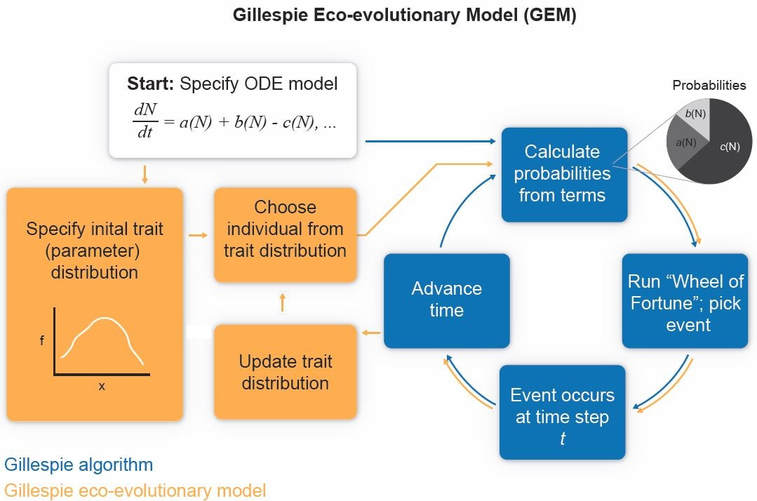
GEMs work by hijacking the Gillespie algorithm (GA) (see schematic below from DeLong and Gibert 2016). The GA is a way of simulating stochastic solutions to ordinary differential equation models (ODEs). In short, the GA turns model rates (such as a rate of foraging) into events with a probability set by the magnitude of the term divided by the sum of all the other terms. For example, if a model has a birth rate term = 9 and a death rate term = 1, the probability of a death at any moment in time is 0.1. At each time step, the GA randomly picks events given their probability (wheel-of-fortune style), advancing time after each step. Individuals are added to or subtracted from a population depending on the event, and a population trajectory emerges as a sequence from these events.
GEMs take this structure and add a side loop. Instead of starting a population with a size of 10, say, we start it with a vector of 10 trait values (i.e., an initial trait distribution). Prior to calculating each probability, an individual trait is drawn from the distribution and used to determine some parameter in the model with a trait-parameter link. For example, background mortality rate can be a power-law function of body mass. So instead of running through the GA with a constant parameter, the parameter updates with each trait at each time step, which therefore determines whether a particular event is more or less likely. As a result, any trait that tends to increase the likelihood of a birth or reduce the likelihood of a death will be favored in the population, causing the trait distribution to move toward higher fitness values. This is what I mean by GEMs being a computational analogue to natural selection, because traits determine fitness in the current landscape and determine the likelihood of specific events.
Heritability is a key issue in GEMs. We use a narrow-sense heritability function where offspring look like their parents. The trait of a new individual added to a population when a birth event occurs is drawn from a distribution of potential traits that depends on the population trait distribution, heritability, and the parent’s value(s). For a derivation of this function, see the methods section in DeLong and Luhring (2018).
Once you have a functioning GEM, you can plot the median of the trajectories alongside the ODE solution to see how trait evolution alters the dynamics. Some nice advantages of GEMs are that 1) you can include any number of traits at one time, 2) all populations in the model can evolve, 3) traits can be connected in myriad ways to the parameters (ecological pleiotropy), and 4) the trait mean and the distribution (or just trait variance) all change over time. As a result, GEMs are a powerful but easy tool for understanding evolution of multiple traits in complex ecological settings (DeLong and Gibert 2016, DeLong and Luhring 2018).
What are GEMs?
GEMs are a computational analogue to natural selection. Key features of GEMs are: 1) fitness-influencing traits of individuals guide population dynamics (but GEMs are not individual-based models), 2) fitness landscapes inherent to a particular model determine which traits will be favored in the population, 3) demographic (including individual) stochasticity influences outcomes, and 4) trait distributions and variance are continually updated.
How do GEMs work?
GEMs work by hijacking the Gillespie algorithm (GA) (see schematic below from DeLong and Gibert 2016). The GA is a way of simulating stochastic solutions to ordinary differential equation models (ODEs). In short, the GA turns model rates (such as a rate of foraging) into events with a probability set by the magnitude of the term divided by the sum of all the other terms. For example, if a model has a birth rate term = 9 and a death rate term = 1, the probability of a death at any moment in time is 0.1. At each time step, the GA randomly picks events given their probability (wheel-of-fortune style), advancing time after each step. Individuals are added to or subtracted from a population depending on the event, and a population trajectory emerges as a sequence from these events.
GEMs take this structure and add a side loop. Instead of starting a population with a size of 10, say, we start it with a vector of 10 trait values (i.e., an initial trait distribution). Prior to calculating each probability, an individual trait is drawn from the distribution and used to determine some parameter in the model with a trait-parameter link. For example, background mortality rate can be a power-law function of body mass. So instead of running through the GA with a constant parameter, the parameter updates with each trait at each time step, which therefore determines whether a particular event is more or less likely. As a result, any trait that tends to increase the likelihood of a birth or reduce the likelihood of a death will be favored in the population, causing the trait distribution to move toward higher fitness values. This is what I mean by GEMs being a computational analogue to natural selection, because traits determine fitness in the current landscape and determine the likelihood of specific events.
Heritability is a key issue in GEMs. We use a narrow-sense heritability function where offspring look like their parents. The trait of a new individual added to a population when a birth event occurs is drawn from a distribution of potential traits that depends on the population trait distribution, heritability, and the parent’s value(s). For a derivation of this function, see the methods section in DeLong and Luhring (2018).
Once you have a functioning GEM, you can plot the median of the trajectories alongside the ODE solution to see how trait evolution alters the dynamics. Some nice advantages of GEMs are that 1) you can include any number of traits at one time, 2) all populations in the model can evolve, 3) traits can be connected in myriad ways to the parameters (ecological pleiotropy), and 4) the trait mean and the distribution (or just trait variance) all change over time. As a result, GEMs are a powerful but easy tool for understanding evolution of multiple traits in complex ecological settings (DeLong and Gibert 2016, DeLong and Luhring 2018).
References
DeLong, J. P., and J. P. Gibert. 2016. Gillespie eco-evolutionary models (GEMs) reveal the role of heritable trait variation in eco-evolutionary dynamics. Ecology and Evolution 6:935–945. LINK
DeLong, J. P., and T. M. Luhring. 2018. Size-dependent predation and correlated life history traits alter eco-evolutionary dynamics and selection for faster individual growth. Population Ecology 60:9–20. LINK
DeLong, J. P., and J. P. Gibert. 2016. Gillespie eco-evolutionary models (GEMs) reveal the role of heritable trait variation in eco-evolutionary dynamics. Ecology and Evolution 6:935–945. LINK
DeLong, J. P., and T. M. Luhring. 2018. Size-dependent predation and correlated life history traits alter eco-evolutionary dynamics and selection for faster individual growth. Population Ecology 60:9–20. LINK