Example 2: Logistic growth
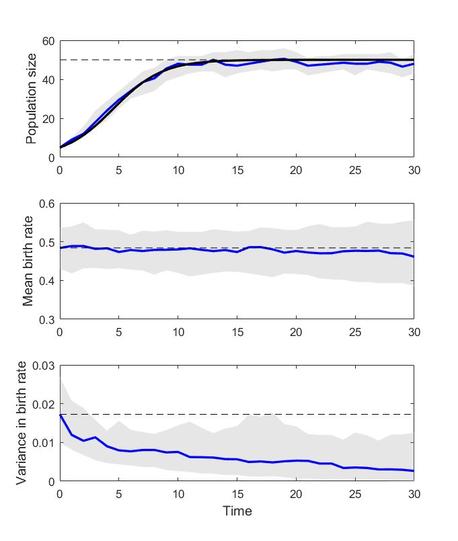
The next simplest GEM we can build is one for logistic growth. The standard ODE for this is dN/dt=rN(1-R/K), where the rate of change in the population size N is proportional to population size with a density dependent rate of increase r(1-R/K). Since there are terms for both births and deaths in this model already, we can proceed without breaking r into births and deaths. The rates then are rN for births and rN^2/K for deaths. Making r the trait under selection, we need to adjust the first line in the code to pass different parameters, line 28 to initiate the population for the different trait, and write out new rate terms on lines 43 and 46. Otherwise the code is the same as for exponential growth. Finally, adjust the names of the file, write a logistic growth model file, and we’re done. You can download a zip folder with the required files here.
What you may have noticed here is that r influences both birth and death rates, so changes in r will have both positive and negative effects on fitness. Not surprisingly, then, there is very little evolution of r in this GEM. If you really wanted to look at the evolution of traits related to births and deaths within a single-species logistic-type model, I would suggest writing a different model with separate birth and death density dependent functions and using that instead.
The next simplest GEM we can build is one for logistic growth. The standard ODE for this is dN/dt=rN(1-R/K), where the rate of change in the population size N is proportional to population size with a density dependent rate of increase r(1-R/K). Since there are terms for both births and deaths in this model already, we can proceed without breaking r into births and deaths. The rates then are rN for births and rN^2/K for deaths. Making r the trait under selection, we need to adjust the first line in the code to pass different parameters, line 28 to initiate the population for the different trait, and write out new rate terms on lines 43 and 46. Otherwise the code is the same as for exponential growth. Finally, adjust the names of the file, write a logistic growth model file, and we’re done. You can download a zip folder with the required files here.
What you may have noticed here is that r influences both birth and death rates, so changes in r will have both positive and negative effects on fitness. Not surprisingly, then, there is very little evolution of r in this GEM. If you really wanted to look at the evolution of traits related to births and deaths within a single-species logistic-type model, I would suggest writing a different model with separate birth and death density dependent functions and using that instead.
